Normed space
A normed vector space is a vector space equipped with a norm. It is a particular case of a metric space.
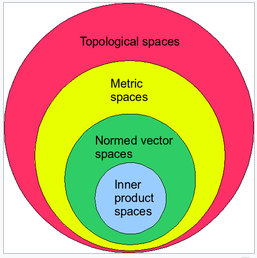
If it is Cauchy complete with respect to the topology induced by the norm, is a Banach space.
Examples of norms:
$$ \begin{aligned} &\|x\|_p =\left(\sum_{i=1}^n\left|x_i\right|^p\right)^{1 / p}, \text { for } p \in[1, \infty) \\ &\|x\|_{\infty} =\max _{i=1: n}\left|x_i\right| \end{aligned} $$Especial class of norms: matrices norms. For example: in the matrix algebra $\mathcal M_n$, given a matrix $A$ we define the infinity norm
$$ \|A\|_{\infty}=\text{max}_{i\leq i\leq n} \sum_{j=1}^n |a_{ij}|. $$It is induced by the infinity norm of $\mathbb R^n$.
Important notion operator on a normed space.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: